![]() >
> ![]()
| SIMULATIONTOOLS TUTORIAL |
Data Representations
SimulationTools uses two different representations of numerical data.
The DataTable is designed for time-series data, and consists of a monotonically-increasing time coordinate and corresponding data values, which can be of any type. The time coordinate does not have to be regularly spaced.
The DataRegion represents an N-dimensional block of data on a uniform grid. The data must consist of real or complex numbers, or the quantities None or Missing[]. The data is stored efficiently in memory. Each point has an associated set of coordinates, and these are specified by giving the origin and spacing of the DataRegion as {ox, oy, ... oz} and {dx, dy, ..., dz}.
Collectively, DataTables and DataRegions are known in SimulationTools as Data Representations. There are many functions for manipulating data representations. Some only make sense for DataTables or DataRegions respectively, but many are defined to work on both types of object.
Many commonly-used Mathematica functions are defined on compatible DataTables and DataRegions (those with the same coordinates), for example Plus (+), Minus (-), Times (*), Divide (/), Sqrt, Power (d^a), Sin, Cos, Tan etc.
Reasons to use Data Representations instead of lists
Data Representations contain coordinate information as well as data; it is frequently desirable to keep the coordinates along with the data.
Mathematical operations defined on Data Representations operate only on the data, as opposed to the data and coordinates, which would be the case if you used a list containing data and coordinates.
Working with Data Representations
Both DataTables and DataRegions can be created from Mathematica lists. They act as opaque objects and are printed in an abbreviated form to avoid cluttering up the notebook with all the numerical data.
Creating DataTables
Using ToDataTable[data], we can create a DataTable from a list of {t, f} pairs:
In[1]:=
![]()
Out[1]=

In[2]:=
![]()
Out[2]=
![]()
t is the independent variable and f is the dependent variable.
The independent variable t should be monotonically increasing, but the interval between points can vary. The "range" of a DataTable is {t1, t2}, where t1 is the first and t2 is the last value of the independent variable.
Creating DataRegions
Using ToDataRegion[data, origin, spacing] we can create a DataRegion object from the (multidimensional) list data. This data is assumed to be in row-major order, eg. data[[ix,iy,iz]] for the case of 3D data. The DataRegion will have an origin and spacing given by the lists origin = {ox, oy, ...} and spacing = {dx, dy, ...}. SimulationTools uses row-major order because that is the convention adopted by Mathematica. Note that this corresponds to “C order”, not “Fortran order”.
In[3]:=
![]()
Out[3]=
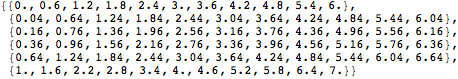
In[4]:=
![]()
Out[4]=
![]()
Mathematical operations on Data Representations
You can use most numerical Mathematica functions which would work on lists of data also on Data Representations. For example,
In[5]:=
![]()
Out[5]=
![]()
In[6]:=
![]()
Out[6]=
![]()
In[7]:=
![]()
Out[7]=
![]()
In[8]:=
![]()
Out[8]=
![]()
In[9]:=
![]()
Out[9]=
![]()
In[10]:=
![]()
Out[10]=
![]()
Here we have created a DataTable for a t coordinate, applied Sin and Cos to it, and formed the sum of their squares to obtain a DataTable which contains the value 1. Note that the Sin and Cos functions operate only on the data part of the DataTable, and do not affect the coordinate part. If you were to do the same with Mathematica lists, the coordinate part would also be operated upon.
(Technically, Data Representations can be used directly with all functions which have the attributes NumericFunction and Listable)
Multi-dimensional DataRegions support the same operations.
In[11]:=
![]()
Out[11]=
![]()
In[12]:=
![]()
Out[12]=
![]()
In[13]:=
![]()
Out[13]=
![]()
In[14]:=
![]()
Out[14]=
![]()
In[15]:=
![]()
Out[15]=
![]()
In[16]:=
![]()
Out[16]=
![]()
Converting between 1D DataRegions and DataTables
A 1D DataRegion can be converted to a DataTable object using ToDataTable[dr].
A DataTable can be converted to a 1D DataRegion using ToDataRegion[dt]. Note that the DataTable should have a uniform spacing.
Properties and data of Data Representations
ToListOfData returns the data in the Data Representation as a nested list.
In[17]:=
![]()
Out[17]=
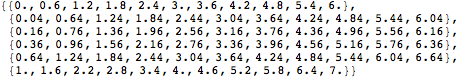
ToListOfCoordinates returns the coordinates of all the points in the Data Representation
In[18]:=
![]()
Out[18]=

ToList returns a list containing all the data and all the coordinates from the Data Representation.
In[19]:=
![]()
Out[19]=

Dimensions returns a list {nx, ny, nz, ...} containing the number of points in each direction.
In[20]:=
![]()
Out[20]=
![]()
MinCoordinates returns the minimum coordinates of the Data Representation.
In[21]:=
![]()
Out[21]=
![]()
MaxCoordinates returns the maximum coordinates of the Data Representation
In[22]:=
![]()
Out[22]=
![]()
CoordinateRanges returns a list of the form {{xmin, xmax}, {ymin, ymax}, {zmin, zmax}, ...} describing the minimum and maximum coordinates of the DataRegion.
In[23]:=
![]()
Out[23]=
![]()
CoordinateSpacings returns the spacing between points in the Data Representation in each direction.
In[24]:=
![]()
Out[24]=
![]()
ArrayDepth returns an integer corresponding to the dimensionality of the data.
In[25]:=
![]()
Out[25]=
![]()
VariableName returns a string containing the name of the DataRegion (DataTables do not have an associated name). This name can be set using the Variable option of ToDataRegion.
In[26]:=
![]()
Interpolation
The Interpolation function has been overloaded to work on Data Representation objects. The resulting function will generically be a function of n variables, where n is the dimensionality of the data.
In[27]:=
![]()
Out[27]=
![]()
In[28]:=
![]()
Out[28]=
![]()
Perform a line integral using the interpolating function:
In[29]:=
![]()
Out[29]=
![]()
Extracting subsets of data
The Part function, i.e. d[[2]] etc, has been overloaded to work on Data Representation objects. You can extract a single value, for example d[[3,8,1]], or a lower-dimensional DataRegion, d[[All,All,12]]. You can also specify ranges of indices: d[[All,3;;8,12]]. Unless the result is a single point, the returned value is always a DataRegion.
The Slab function allows you to extract part of a DataRegion by coordinate rather than by index, as in Part above. For example, if you have a 3D DataRegion and you want to obtain a slice in the xy plane at z = 3.5, you can use d[[All,All,3.5]]. You can also specify coordinate ranges: d[[-2.0;;+2.0, -2.0;;+2.0, 3.5]].
In[30]:=
![]()
Out[30]=
![]()
In[31]:=
![]()
Out[31]=
![]()
Merging DataRegions
Multiple DataRegions d1, d2, ... can be merged into a single enclosing one using
![]()
This is not yet supported for DataTables.
Plotting
| ListPlot | ArrayPlot |
| ListLinePlot | ListPlot3D |
| ListDensityPlot | ListContourPlot |
Plotting functions.
Several standard Mathematica plotting functions have been modified to work also with Data Representations.
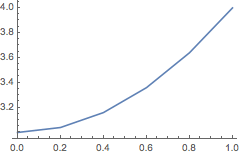
ListPlot and ListLinePlot can be used with 1-dimensional DataRegions and DataTables.
In[32]:=
![]()
Out[32]=
ListDensityPlot, ArrayPlot, ListPlot3D and ListContourPlot can be used with 2-dimensional DataRegions. The DataRange option is computed automatically from the coordinate information in the DataRegion.
In[33]:=
![]()
Out[33]=

In[34]:=
![]()
Out[34]=
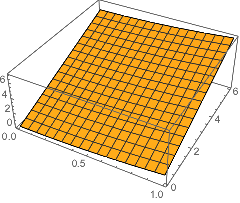
In[35]:=
![]()
Out[35]=